[알고리즘] 삼성 SW 역량 테스트(코딩 테스트) 자주 나오는 알고리즘 유형 정리

감자 개발자 2024. 4. 8. 21:27

2024. 4. 8. 21:27

728x90

코테 준비하면서 까먹은 알고리즘 유형들이 너무 많아서 파이썬 코드로 다시 정리해 놓으려고 한다.

1. 입력받기

삼성 코테에서는 사용할 모든 input에 대해서 미리 정의해 놓은 답지를 제공한다. 따라서, 크게 필요는 없지만...

1.1 기본 저장

기본적으로 저장은 문자열로 저장된다.

a = input()

1.2 입력과 형 변환

입력과 동시에 정수로 형 변환

a = int(input())

1.3 split()

파라미터를 주지 않으면, 공백 문자를 기준으로 잘라주는 내장함수.

a = input().split()

1.4 map()

map(func, x)의 형태로 사용하는 방식으로 x의 각 요소에 func을 적용시켜 주는 함수이다.

a = list(map(int, input().split()))

1.5 가변인자

n개까지는 리스트로 받고, 마지막을 정수형으로 받는 등의 형태를 할 수 있다.

*a, b = map(int, input().split())

1.6 1차원 배열

a = list()
for _ in range(10):
    a.append(0)

a = [ 0 for _ in range(10) ]

a = [ 0 ] * 10

1.7 2차원 배열

a = [[0] * m for _ in range(n) ]   # n x m 배열

1.8 반복해서 입력받기

L, A, B, C, D = [ int(input()) for _ in range(5) ]

1.9 2차원 배열 입력받기

n, m = map(int, input().split())
a = [ list(map(int, input())) for _ in range(n) ]

공백으로 구분되어 있는 경우

n, m = map(int, input().split())
a = [ list(map(int, input().split())) for _ in range(n) ]

2. 정렬

2.1 오름 차순 정렬하기

a가 오름차순으로 변경되는 방법

a = [1, 5, 7, 4, 6]
a.sort()

a는 변경시키지 않고 반환 값만 정렬해서 넘겨주는 방식

a = [1, 5, 7, 4, 6]
b = sorted(a)

2.2 내림차순 정렬하기

a = [1, 5, 7, 4, 6]
a.sort(reverse=True)

2.3 기준에 따라 정렬하기

x좌표를 오름차순으로,
x좌표가 같다면 y좌표를 오름차순으로

a = [list(map(int, input().split())) for _ in range(5)]
a.sort(key = lambda x: x[1])

y좌표를 오름차순으로
y좌표가 같다면 x좌표를 내림차순으로

a = [list(map(int, input().split())) for _ in range(5)]
a.sort(key = lambda x: (x[1], -x[0]))

3. 큐, 스택, 덱(Queue, Stack, Deque)

3.1 Queue

Queue란, 먼저 들어온 데이터가 먼저 나가는 구조로 FIFO를 띄는 자료구조이다.

push: 큐의 가장 마지막에 데이터를 넣는 연산
pop: 큐의 가장 앞의 데이터를 제거하는 연산
front: 큐의 가장 앞의 값을 확인하는 연산
empty: 큐가 비어있는지 확인하는 연산

python에서 제공하는 함수에는

put(x) : x를 큐의 가장 뒤에 넣는다
get() : 큐의 가장 앞에 있는 정수를 빼고 그 값을 반환한다
qsize() : 큐에 들어있는 정수의 개수를 반환한다
empty() : 큐에 비어있으면 True, 아니면 False를 반환한다

이 있다.

import queue
q = queue.Queue()

3.2 Stack

Stack이란, 나중에 들어온 데이터가 먼저 나가는 구조로 LIFO를 띄는 자료구조이다.

push: 스택의 가장 마지막에 데이터를 넣는 연산
pop: 스택의 가장 마지막의 데이터를 제거하는 연산
top: 스택의 가장 마지막의 값을 확인하는 연산
empty: 스택이 비어있는지 확인하는 연산
size: 스택의 크기를 확인하는 연산

python에서 제공하는 함수에는

append(x): 리스트의 가장 마지막에 x를 추가한다.
pop(): 리스트의 가장 마지막 원소를 제거한다.

이 있다.

Stack은 모듈로 존재 하지 않고, 리스트를 통해 간접 구현한다.

3.3 Deque

Deque란, 양방향 Queue라는 의미의 자료구조이다. 앞 뒤 모두 삽입 가능하고 삭제 가능하다.

append(x): 덱의 가장 뒤에 x를 삽입한다.
appendleft(x): 덱의 가장 앞에 x를 삽입한다.
pop(): 덱의 가장 마지막 원소를 제거하며 반환한다.
popleft(): 덱의 가장 처음 원소를 제거하며 반환한다.

from collections import deque
dq = deque()

4. 순열과 조합

실제 시험에서 itertools 모듈이 사용 불가능할 수 있다. 직접 구현 방법도 외워 놓자.

# 중복 없는 순열
from itertools import permutations
# 중복 없는 조합
from itertools import combinations
# 중복 있는 순열 / 각 집단에서 추출
from itertools import product
# 중복 있는 조합
from itertools import combinations_with_replacement

4.1 직접 구현

# 순열 : n개 중에서 중복없이 r개를 뽑음, 이때 순서 상관있음(순서가 다르고 원소가 같으면 다른 걸로 침)
def permutations(arr, r):
    for i in range(len(arr)):
        if r == 1:
            return [arr[i]]
        else:
            for next in permutations(arr[:i] + arr[i+1:], r-1):
                yield [arr[i]] + next

# 조합 : n개 중에서 중복없이 r개를 뽑음, 이때 순서 상관없음(순서가 다르고 원소가 같으면 같은 걸로 침)
def combinations(arr, r):
    for i in range(len(arr)):
        if r == 1:
            return [arr[i]]
        else:
            for next in combinations(arr[i+1:], r-1):
                yield [arr[i]] + next

# 중복조합 : n개 중에서 중복 포함하여 r개를 뽑음, 이때 순서 상관없음
def combinations_with_replacement(arr, r):
    for i in range(len(arr)):
        if r == 1:
            return [arr[i]]
        else:
            for next in combinations_with_replacement(arr[i:], r-1):
                yield [arr[i]] + next

# 중복 순열 : n개 중에서 중복 포함하여 r개를 뽑음, 이때 순서 상관있음
def product(arr, r):
    for i in range(len(arr)):
        if r == 1:
            return [arr[i]]
        else:
            for next in product(arr, r-1):
                yield [arr[i]] + next

4.2 중복 없는 순열

from itertools import permutations
print(list(permutations([1,2,3], 3)))

4.3 중복 없는 조합

from itertools import combinations

n, m = map(int, input().split())
c = list(combinations(range(1, n+1), m))

for x in c:
   print(*x)

4.4 중복 있는 순열 / 각 집단에서 추출 구현

product 함수를 통해 구현

from itertools import product
product([1,2,3], [4,5,6]) # 각 리스트 별로 한 개씩 추출한다.
product([1,2,3], repeat = 2)

4.5 중복 있는 조합

from itertools import combinations_with_replacement as com

n, m = map(int, input().split())
c = list(com(range(1, n+1), m))

for x in c:
    print(*x)

5. BFS와 DFS

여기서 무조건 한 문제가 나온다.

5.1 이론 설명

BFS는 Breadth First Search로 너비 우선 탐색이라는 뜻이다.

DFS는 Depth First Search로 깊이 우선 탐색이라는 뜻이다.

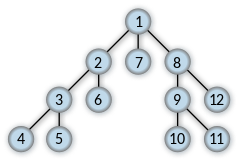
가장 중요한 점은 그래프를 모두 탐색하는 알고리즘이다.

5.2 입력받는 방식

인접 행렬 방식

# 배열을 통한 그래프 표현 방법
n, m, v = map(int, input().split()) #정점의 개수, 간선의 개수, 시작 번호

a = [[0]*(n+1) for _ in range(n+1)]

for _ in range(m):
    x, y = map(int, input().split())
    a[x][y] = 1
    a[y][x] = 1

for x in a:
    print(x)

인접 리스트 방식

n, m, v = map(int, input().split()) #정점의 개수, 간선의 개수, 시작 번호

a = [list() for _ in range(n+1)]
for _ in range(m):
    x, y = map(int, input().split())
    a[x].append(y)
    a[y].append(x)

for x in a:
    print(x)

5.3 BFS

import queue
n, m, v = map(int, input().split()) # 정점의 개수, 간선의 개수, 시작 번호

a = [list() for _ in range(n+1)]
for _ in range(m):
    x, y = map(int, input().split())
    a[x].append(y)
    a[y].append(x)

for x in a:
    x.sort()

chk = [False]*(n+1)
q = queue.Queue()
q.put(v)
chk[v] = True

import queue
n, m, v = map(int, input().split())    # 정점의 개수, 간선의 개수, 시작 번호

a = [list() for _ in range(n+1)]
for _ in range(m):
    x, y = map(int, input().split())
    a[x].append(y)
    a[y].append(x)

for x in a:
    x.sort()

chk = [False]*(n+1)

# BFS 함수 구현 
def bfs(start):
    q = queue.Queue()
    q.put(start)
    chk[start] = True

    while not q.empty():               
        now = q.get()                 # 큐에서 가장 앞으 노드를 꺼내온다.
        print(now, end=" ")           # 해당 노드를 방문한다는 의미로 출력한다.
        for next in a[now]:           # 방문한 노드의 인접 노드들을 for문을 통해 next에 저장한다.
            if not chk[next]:         # 인접 노드가 체크가 되어있지 않다면
                chk[next] = True      # 체크를 해주고,
                q.put(next)           # 인접 노드를 큐에 넣어준다. 
    print()

bfs(v) # bfs 함수 실행

5.4 DFS

n, m, v = map(int, input().split()) #정점의 개수, 간선의 개수, 시작 번호

a = [list() for _ in range(n+1)]
for _ in range(m):
    x, y = map(int, input().split())
    a[x].append(y)
    a[y].append(x)

for x in a:
    x.sort()

chk = [False]*(n+1)

n, m, v = map(int, input().split()) #정점의 개수, 간선의 개수, 시작 번호

a = [list() for _ in range(n+1)]
for _ in range(m):
    x, y = map(int, input().split())
    a[x].append(y)
    a[y].append(x)

for x in a:
    x.sort()

chk = [False]*(n+1)

def dfs(node):
    chk[node] = True
    print(node, end=" ")

    for next in a[node]:
        if not chk[next]:
            dfs(next)

dfs(v)
print()

5.5 BFS, DFS 총 코드

import queue
n, m, v = map(int, input().split()) #정점의 개수, 간선의 개수, 시작 번호

a = [list() for _ in range(n+1)]
for _ in range(m):
    x, y = map(int, input().split())
    a[x].append(y)
    a[y].append(x)

for x in a:
    x.sort()

def bfs(start):
    q = queue.Queue()
    q.put(start)
    chk[start] = True

    while not q.empty():
        now = q.get()
        print(now, end=" ")
        for next in a[now]:
            if not chk[next]:
                chk[next] = True
                q.put(next)
    print()

def dfs(node):
    chk[node] = True
    print(node, end=" ")

    for next in a[node]:
        if not chk[next]:
            dfs(next)

chk = [False]*(n+1)
dfs(v)
print()
chk = [False]*(n+1)
bfs(v)

6. 백트래킹 (Backtracking)

6.1 백트래킹 VS DFS 비교

백트래킹
- 어떤 노드에서 출발하는 경로가 그 해결책으로 이어질 것 같지 않으면 더 이상 경로를 탐색하지 않음으로써 시도 횟수 감소
- 불필요한 경로의 조기 차단
- N! 가지의 경우의 수를 가진 문제에 대해 백트레킹에 가하면 일반적으로 경우의 수가 줄어들지만 최악의 경우는 처리 불가능
- 모든 후보를 검사하지 않음
DFS
- 모든 경로를 추적
- N! 가지의 경우의 수를 가진 문제에 대해 깊이 우선 탐색을 이용하면 처리 불가능
- 모든 후보를 검사

6.2 백트래킹 구현

기본 구현

def 재귀함수(n):
	if 정답이면 :
		출력 or 저장
	else : 정답이 아니면 :
		for 모든 자식 노드에 대해서:
			if 답의 가능성이 있으면:
				자식노드로이동
				재귀함수(n+1)
				부모노드로 이동

답 조건 확인하면서 구현

def 백트래킹(n):
	if 정답이면 :
		출력 or 저장
	else :
		for 모든 자식 노드에 대해 :
			if 유망한지확인(m) :
				자식노드로 이동
				백트래킹(n+1)
				부모노드로 이동

def 답에 가까운지 확인(m):
	if 조건에 안맞으면 :
		return False
	return True

0. 참고자료

https://m.blog.naver.com/PostList.naver?blogId=wpghks7&categoryName=삼성% 20SW역량테스트&categoryNo=4&logCode=0

알파카고수 : 네이버 블로그

당신의 모든 기록을 담는 공간

m.blog.naver.com

https://velog.io/@dust_potato/python-itertools-algorithm-직접-구현하기

[python] itertools algorithm 직접 구현하기

velog.io

https://edder773.tistory.com/75

[파이썬] 탐색 알고리즘 정리 - 백트래킹

백트래킹 (*Notion AI의 설명) 백트래킹(Backtracking)은 해결책을 구하기 위해 모든 가능성을 시도해보는 것이 아니라, 해결책에 대한 후보군을 구성하고 그 후보군이 문제의 조건을 만족하는지 여부

edder773.tistory.com

728x90

저작자표시 비영리 변경금지 (새창열림)

'컴퓨터 > Algorithm' 카테고리의 다른 글

[삼성 D-7] 삼성 SW 역량테스트 2015 하반기 1번 문제 : 바이러스 검사 (0)	2024.04.08
[헷갈리는 python - 01] 반복문 제어 : break, continue, pass (0)	2024.04.08

감자 개발자